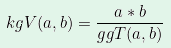Brüche gleichnamig machen - Rechner

Über den Rechner

Mit diesem Rechner lassen sich Brüche gleichnamig machen. Für die Berechnung des gemeinsamen Nenners wird wahlweise entweder das Produkt der Nenner oder das kleinste gemeinsame Vielfache verwendet. Es wird immer sowohl die Lösung als auch der Lösungsweg angezeigt.

Gleichnamige Brüche

Brüche werden gleichnamig genannt, wenn sie den gleichen Nenner haben. Um Brüche addieren oder subtrahieren zu können, müssen sie vorher gleichnamig gemacht werden.

Wie macht man Brüche gleichnamig?

Um Brüche gleichnamig zu machen, sucht man zuerst ein gemeinsames Vielfaches und erweitert die Brüche danach, sodass sie hinterher alle das gemeinsame Vielfache im Nenner stehen haben.

Beispiel:

Es sollen die folgenden 2 Brüche gleichnamig gemacht werden:
2
3
und
1
4

Es muss ein gemeinsames Vielfaches von 3 und 4 gefunden werden. Das ist zum Beispiel 12.

Danach muss
2
3
um 4 erweitert werden und
1
4
um 3, damit hinterher beide Brüche im Nenner eine 12 stehen haben.
  • 2
    3
    =
    2 · 4
    3 · 4
    =
    8
    12
  • 1
    4
    =
    1 · 3
    4 · 3
    =
    3
    12

gemeinsames Vielfaches finden

Um ein gemeinsames Vielfaches zu finden, gibt es verschiedene Methoden. Jede hat ihre Vor- und Nachteile.

ein Nenner ist Vielfaches der anderen Nenner:

Wenn der Nenner von einem Bruch Vielfaches vom Nenner des anderen Bruchs (oder der andere Brüche) ist, dann kann er als das gemeinsame Vielfache verwendet werden, auf den die Brüche im Nenner gebracht werden.

Beispiel:

Es sollen die folgenden 2 Brüche gleichnamig gemacht werden:
3
4
und
5
12

12 ist ein Vielfaches von 4. Also wird
3
4
um 3 erweitert, damit hinterher eine 12 im Nenner steht:

3
4
=
3 · 3
4 · 3
=
9
12

Produkt der Nenner:

Eine einfache Methode, um ein gemeinsames Vielfaches zu finden, ist die Nenner zu multiplizieren. Dies lässt sich in der Praxis leicht durchführen, häufig werden die Zahlen in den Brüchen dadurch aber größer als unbedingt nötig.

Beispiel:

Es sollen die folgenden 2 Brüche gleichnamig gemacht werden:
3
8
und
5
12

Das Produkt der beiden Nenner ist 8 · 12 = 96. Also wird
3
8
um 12 erweitert und
5
12
um 8.
  • 3
    8
    =
    3 · 12
    8 · 12
    =
    36
    96
  • 5
    12
    =
    5 · 8
    12 · 8
    =
    40
    96

Ein gemeinsamer Nenner wäre aber auch 24 gewesen. In dem Fall wären die Brüche in
9
24
und
10
24
umgewandelt worden, womit sich normalerweise leichter hätte weiterrechnen lassen.

Vielfache auflisten:

Eine weitere Methode ist, dass man für beide Nenner die Vielfachen berechnet, bis man eine Zahl gefunden hat, die Vielfaches von beiden Nennern ist. Wenn man die Vielfachen in aufsteigender Reihenfolge berechnet ohne Vielfache auszulassen, dann findet man durch dieses Vorgehen das kleinste gemeinsame Vielfache.

Beispiel:

Es sollen die folgenden 2 Brüche gleichnamig gemacht werden:
5
8
und
1
6
Die ersten Vielfachen von 8 sind: 8, 16, 24, 32, ...
Die ersten Vielfachen von 12 sind: 6, 12, 18, 24, 30, ...

Das kleinste gemeinsame Vielfache ist somit 24.

  • 5
    8
    =
    5 · 3
    8 · 3
    =
    15
    24
  • 1
    6
    =
    1 · 4
    6 · 4
    =
    4
    24

Wenn nur wenige Vielfache der Nenner berechnet werden müssen, bis das kleinste gemeinsame Vielfache gefunden wurde, dann ist es in der Praxis häufig sinnvoll diese Methode zu verwenden. Es kann aber auch passieren, dass man zuerst sehr viele Vielfache berechnen müsste, bis man das kleinste gemeinsame Vielfache erreicht hat. Zum Beispiel ist 204 das kleinste gemeinsame Vielfache von 4 und 102 und die 4 hat bis 204 (einschließlich der 4 und der 204) 51 Vielfache.

Primfaktorzerlegung:

Das kleinste gemeinsame Vielfache der Nenner lässt sich auch mit der Hilfe von Primfaktorzerlegungen bestimmen. Dafür werden zuerst, für die Zahlen in den Nennern, die Primfaktorzerlegungen durchgeführt und in die kanonische Darstellung (gleiche Primfaktoren zu Potenzen zusammenfassen) gebracht. Danach wird für jede Zahl, die in mindestens einer Primfaktorzerlegung als Primfaktor auftaucht, die Potenz markiert, bei welcher die Zahl in der Basis steht und der Exponent am größten ist. Am Ende wird von den markierten Potenzen bzw. Zahlen das Produkt gebildet.

Beispiel:

Es sollen die folgenden 2 Brüche gleichnamig gemacht werden:
15
360
und
5
54

In ihre Primfaktoren zerlegt gilt für 360 und 54:

360=2 · 2 · 2 · 3 · 3 · 5
 =23 · 32 · 5
54=2 · 3 · 3 · 3
 =2 · 33

Die 2 kommt am häufigsten in der Primfaktorzerlegung von 360 vor, die 3 am häufigsten in der Primfaktorzerlegung von 54 und die 5 kommt nur in der Primfaktorzerlegung von 360 vor. Also berechnet man das kleinste gemeinsame Vielfache wie folgt:

kgV(360, 54)=23 · 33 · 5
 =8 · 27 · 5
 =1080

Danach werden die Brüche so erweitert, dass in den Nennern 1080 steht:

  • 15
    360
    =
    15 · 3
    360 · 3
    =
    45
    1080
  • 5
    54
    =
    5 · 20
    54 · 20
    =
    100
    1080

euklidischer Algorithmus:

Für den größten gemeinsamen Teiler und das kleinste gemeinsame Vielfache besteht der folgende Zusammenhang:

Formel zur Berechnung vom kgV mit dem ggT

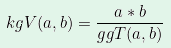
Für die Berechnung vom ggT von 2 Zahlen kann der euklidische Algorithmus verwendet werden.

Beispiel:

Es sollen die folgenden 2 Brüche gleichnamig gemacht werden:
10
21
und
5
15

Zuerst wird der ggT der beiden Nenner mit der Hilfe vom euklidischen Algorithmus berechnet:

21:15=1Rest6
15:6=2Rest3
6:3=2Rest0

Ergebnis: ggT(21, 15) = 3

Danach wird das kgV berechnet, indem das Produkt der beiden Nenner durch den ggT der beiden Nenner geteilt wird:

kgV(15, 21)=
15∙21
ggT(15, 21)
 =
315
3
 =105

Dann werden die Brüche erweitert, sodass sie 105 im Nenner stehen haben:

  • 10
    21
    =
    10 · 5
    21 · 5
    =
    50
    105
  • 5
    15
    =
    5 · 7
    15 · 7
    =
    35
    105

gute Erklärvideos auf YouTube:

Seite teilen:FacebookTwitter