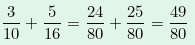Über den Rechner
Mit diesem Rechner lässt sich das kleinste gemeinsame Vielfache (kurz kgV) von 2 oder mehr Zahlen berechnen. Es werden nur Zahlen akzeptiert, die größer als 0 sind. Es kann ausgewählt werden, ob die Berechnung mit der Hilfe von Primfaktorzerlegungen, Reihen von Vielfachen oder dem mit dem euklidischen Algorithmus berechneten ggT durchgeführt werden soll.
Was ist das kgV?
Eine Zahl a ist Vielfaches von einer Zahl b, wenn es eine ganze Zahl k gibt, sodass a = k · b gilt. Wenn zusätzlich noch für eine Zahl c gilt, dass es eine ganze Zahl l gibt, sodass a = l · c gilt, dann ist a ein gemeinsames Vielfaches von b und c. Wenn es keine kleinere Zahl gibt, die gemeinsames Vielfaches von b und c ist, dann ist a das kleinste gemeinsame Vielfache von b und c.
kgV mit Primfaktorzerlegungen
Jede ganze Zahl größer als 1 lässt sich als Produkt von Primzahlen darstellen. Die einzelnen Zahlen dieses Produkts nennt man Primfaktoren.
Zum Beispiel ist die Primfaktorzerlegung der Zahl 270: 2 · 3 · 3 · 3 · 5
Und von der Zahl 2352 ist die Primfaktorzerlegung: 2 · 2 · 2 · 2 · 3 · 7 · 7
Die Primfaktorzerlegungen lassen sich mit Potenzen auch etwas kompakter aufschreiben:
Primfaktorzerlegungen 270: 2 · 33 · 5
Primfaktorzerlegungen 2352: 24 · 3 · 72
Nun sieht man sich für jede Zahl in den Primfaktorzerlegungen an, in welcher Primfaktorzerlegung sie den höheren Exponenten haben und in dieser Primfaktorzerlegung wird die Zahl samt Exponent markiert.
Die 2 hat in der ersten Primfaktorzerlegung den Exponenten 1 und in der zweiten den Exponenten 4. Also wird 24 in der zweiten Primfaktorzerlegung markiert. Die 3 hat hingegen in der ersten Primfaktorzerlegung den höheren Exponenten und wird somit in der ersten Primfaktorzerlegung markiert. 5 und 7 kommen jeweils nur in einer Primfaktorzerlegung vor und werden deshalb in dieser markiert.
Primfaktorzerlegungen 270: 2 · 33 · 5
Primfaktorzerlegungen 2352: 24 · 3 · 72
Um das kgV zu erhalten müssen nun das Produkt aus allen markierten Potenzen berechnet werden.
kgV(270, 2352) = 24 · 33 · 5 · 72 = 105.840
kgV mit Reihen von Vielfachen
Bei dieser Methode schreibt man für beide Zahlen, beginnend mit den Zahlen selber, die Vielfachen auf. Wenn man das kgV von 2 Zahlen a und b bestimmen möchte, berechnet man also [1·a, 2·a, 3·a,...] und für b [1·b, 2·b, 3·b,...]. Dies macht man so lange, bis eine Zahl in beiden Reihen auftaucht. Wichtig ist, dass man die Vielfachen in der richtigen Reihenfolge aufschreibt, weil sonst nicht garantiert ist, dass das gefundene Vielfache das kleinste Vielfache ist. Auslassen darf man Vielfache nur, wenn man ausschließen kann, dass sich unter den den ausgelassenen Vielfachen das kgV befindet. Zum Beispiel muss man, wenn man das kgV von 3 und 100 berechnen möchte, nicht zwingend alle Vielfachen von 3 berechnen, die kleiner als 100 sind, weil diese kein Vielfaches von 100 sein können.
Als Beispiel soll das kleinste gemeinsame Vielfache von 10 und 16 bestimmt werden.
Vielfache von 10: [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...]
Vielfache von 16: [16, 32, 48, 64, 80, 96, ...]
Die Zahl 80 ist die erste Zahl, die in beiden Reihen vorkommt und ist somit das kleinste gemeinsame Vielfache.
kgV mit ggT
Das kgV lässt sich auch mit der Hilfe vom ggT bestimmen. Es gibt den folgenden Zusammenhang zwischen dem ggT und dem kgV:
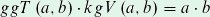
Wenn man nun durch den ggT teilt, erhält man die folgende Formel:
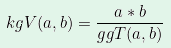
Um das kgV zu berechnen, kann man also zuerst den größten gemeinsamen Teiler berechnen (zum Beispiel mit dem euklidischen Algorithmus) und das Ergebnis setzt man in die Formel ein.
Als Beispiel soll das kleinste gemeinsame Vielfache von 10 und 16 berechnet werden. Zuerst berechnet man den ggT mit dem euklidischen Algorithmus:
| 16 | : | 10 | = | 1 | Rest | 6 |
| 10 | : | 6 | = | 1 | Rest | 4 |
| 6 | : | 4 | = | 1 | Rest | 2 |
| 4 | : | 2 | = | 2 | Rest | 0 |
Ergebnis: ggT(10, 16) = 2
Als nächstes wird das Ergebnis genutzt, um das kgV zu berechnen:
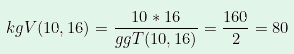
kgV von mehr als 2 Zahlen
Aber wie berechnet man das kleinste gemeinsame Vielfache von mehr als 2 Zahlen?
mit Primfaktorzerlegung:
Das Berechnen vom kgV von mehr als 2 Zahlen mit der Primfaktorzerlegung funktioniert vom Prinzip her genau so, wie das Berechnen vom kgV von 2 Zahlen. Man führt für jede Zahl eine Primfaktorzerlegung durch, markiert sich für jede Zahl die als Basis mindestens einer Primfaktorzerlegung vorkommt die Potenz mit dem höchsten Exponenten und bildet dann das Produkt aller markierten Potenzen.
mit Reihen von Vielfachen:
Auch das Berechnen vom kgV mit Reihen von Vielfachen funktioniert so, wie mit 2 Zahlen. Man berechnet für alle Zahlen so lange weitere Vielfache, bis ein Vielfaches in jeder Reihe vorkommt.
mit ggT
Um das kgV aus 3 Zahlen a, b und c zu berechnen kann man zuerst das kgV von a und b mit der Hilfe vom ggT berechnen. Danach berechnet man das kgV von dem Ergebnis und c, um das kgV von allen 3 Zahlen zu erhalten. Auf diese Weise kann man das kgV von beliebig vielen Zahlen berechnen. Dabei ist zu beachten, dass die Reihenfolge, in der man die kgVs berechnet egal ist. Man könnte auch zuerst das kgV von b und c berechnen und danach das kgV vom Ergebnis und a.
Beispiel:
Als Beispiel möchte man das kleinste gemeinsame Vielfache von 4, 10, 15 und 18 berechnen.
Schritt 1: Zuerst wird mit der Hilfe vom ggT das kgV von 4 und 10 berechnet. Das ist 20.
Schritt 2: Als nächstes wird das kgV von 20 und 15 berechnet. Das ist 60.
Schritt 3: Dann wird das kgV von 60 und 18 berechnet. Das ist 180.
Somit gilt: kgV(4, 10, 15, 18) = 180
Was kann man mit dem kgV machen?
Das kgV kann genutzt werden, um 2 Brüche gleichnamig zu machen. 2 Brüche nennt man gleichnamig, wenn sie den gleichen Nenner haben. Wenn man 2 Brüche addieren oder subtrahieren möchte, ist es wichtig, dass die Nenner beider Brüche gleich sind.
Wenn man 2 Brüche gleichnamig machen möchte, kann man das kgV von beiden Nennern berechnen und erweitert danach beide Brüche, sodass sie hinterher das kgV als Nenner haben.
Als Beispiel möchte man die folgendes berechnen:
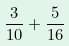
Um die beiden Brüche gleichnamig zu machen muss man das kgV von 10 und 16 berechnen. Das beträgt 80. Danach erweitert man beide Brüche so, dass sie als Nenner 80 haben und führt danach die Addition durch: